The story of 𝞹
What is it? Why is it important? How did we calculate it, and why we need to stop calculating it?
We've all studied 𝞹 in our geometry classes. It's 3.14, or you might have used it as 22/7 in calculations.
But what is this number?
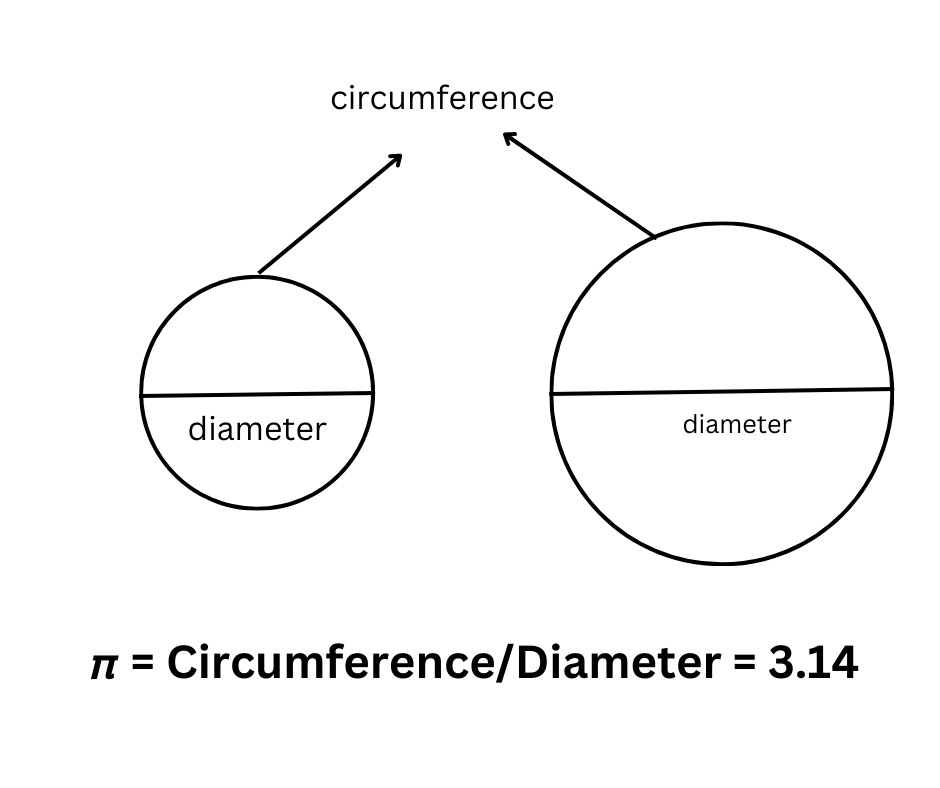
𝞹 is the ratio of the circumference (distance around a circle) to the diameter (distance across a circle).
For any circle, regardless of its size, this ratio remains the same. Drawing a big or small circle results in the circumference changing in proportion to the diameter.
The value of 𝞹 signifies that it takes 3 whole and a little bit more diameters to cover the circle's perimeter.
You can conduct an easy DIY experiment by taking a piece of string, curving it into a circle, and measuring the diameter, and the length of the string (circumference). Dividing the two will yield a value close to 3.1415. Any small difference can be attributed to measurement errors.
Why is 𝞹 important?
This ratio is crucial because it describes not only circles but all curves in linear terms. All curves can be thought of as small sections of a larger circle, allowing us to describe periodic oscillations and electromagnetic waves, among other phenomena.
For example, we know the area of a circle is 𝞹r^2. We arrive at this formula by dividing the circle into thin slices and arranging them to form a rectangle with sides equal to half the circumference (𝞹r) and the radius (r). The area of the rectangle is the same as the area of the circle, which equals 𝞹r^2. Now the area of different sectors of a circle can be defined using this.
The reason we don't just use the value 3.14 is that 𝞹 is an irrational number, meaning its decimal expansion is never-ending and non-repeating (3.14159265358...). It cannot be expressed as 22/7 or any other fraction accurately.
Therefore, we represent it with the Greek letter 𝞹 (pi), first used by William Jones in 1706.
How was 𝞹 calculated?
The concept of 𝞹 and its significance in circles had been discovered by the Babylonians and ancient Egyptians around 4000 years ago. They calculated it quite accurately for their time (around 3.12).
Some people think that it may have been used by the Egyptians to design the Pyramids of Giza (or maybe the aliens did it who knows?).
Later, Archimedes (the running–around–naked–shouting “Eureka!” guy) calculated it through his “method of exhaustion”.
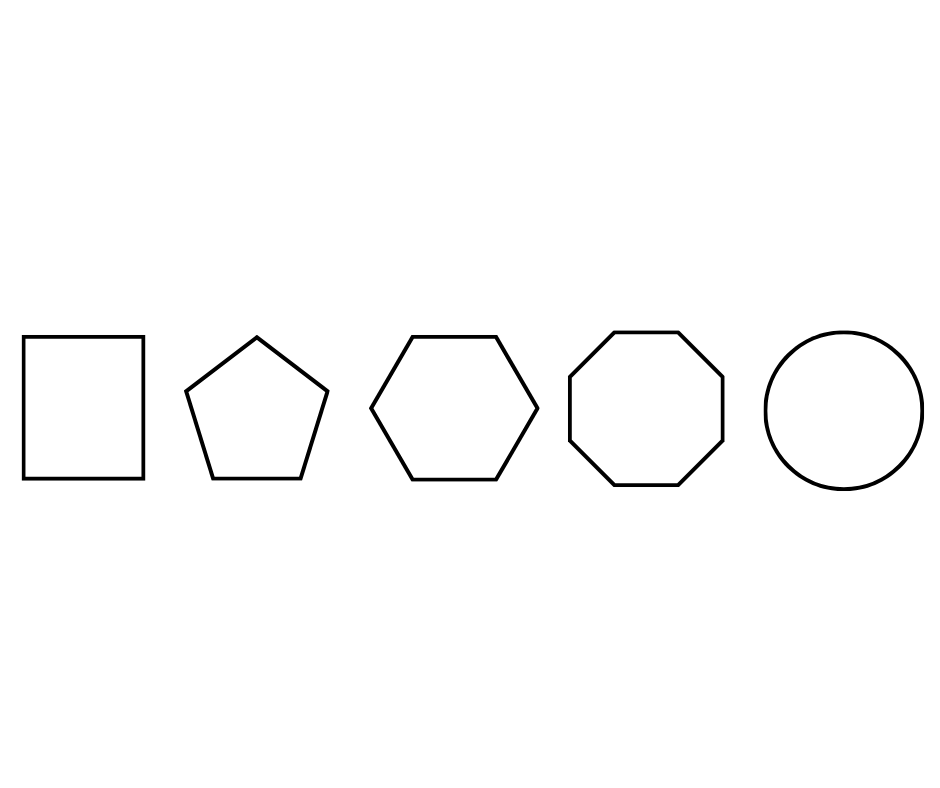
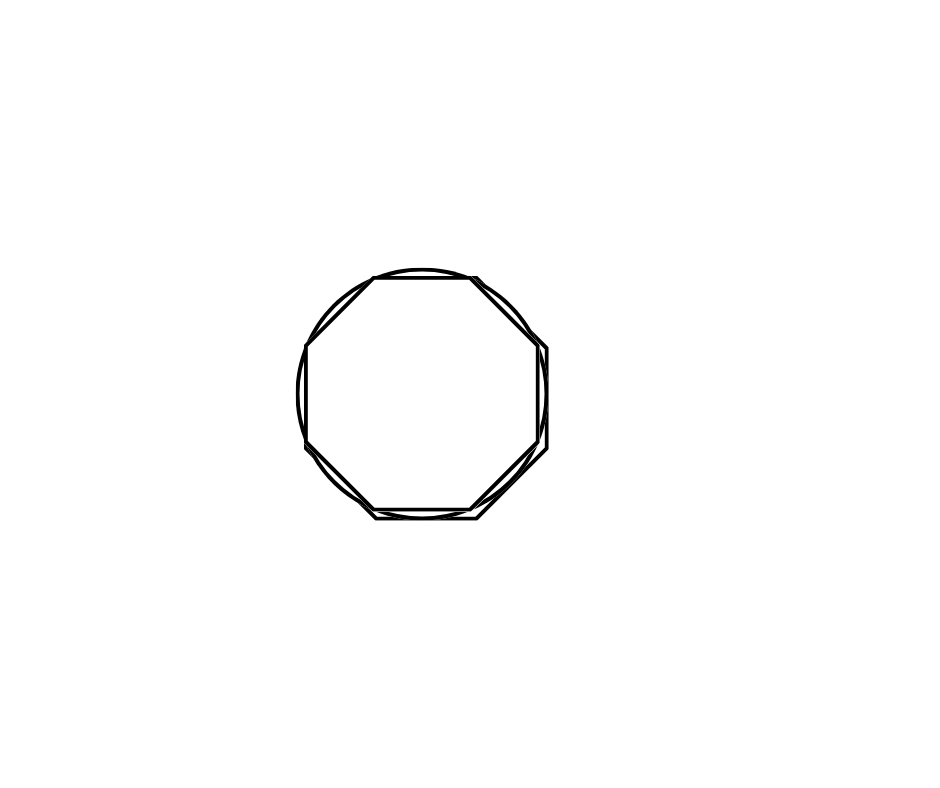
Archimedes thought of a square as similar to a circle. Before you think, “What an idiot! A square is obviously different from a circle,” remember, this guy was a genius. A square IS similar to a circle if you imagine its edges to be curved.
As the number of sides of a polygon increases (e.g., a pentagon, hexagon, heptagon, an octagon), the shape becomes more similar to a circle.
Thus, a circle can be imagined as a polygon with N number of sides, where N is so extremely large that each side is infinitesimally small which appears as curves with no edges.
Archimedes Method
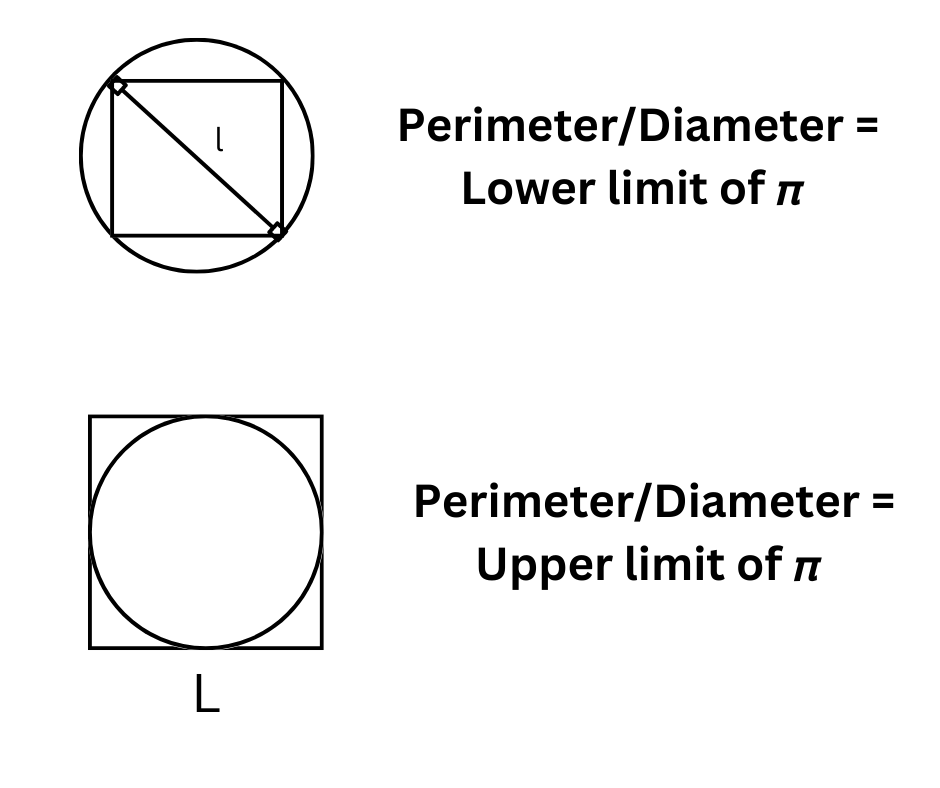
To calculate the ratio of circumference and diameter, you could inscribe a square inside of a circle, calculate the ratio of its perimeter and diagonal, and do the same with the square outside the circle touching it by taking the diameter as a side.
This would give us a lower and upper limit of the value of 𝞹.
As we keep increasing the number of sides of the polygon we do these calculations with, slowly the sides of the polygon will start overlapping with the circle.
Now you know why this is called the “method of exhaustion”.
Archimedes got up to 96 sides, getting the value of 𝞹 to between 3.1408 and 3.1429. With the Indian, Persian, and Chinese mathematicians joining in we got the value of 𝞹 we use most commonly today 3.1415.
However, the really absurd calculations began with the idea of using infinite series by Indian and European mathematicians.
Sir Isaac Newton started to calculate 𝞹 using infinite series because he was bored after being stuck at home, away from Cambridge due to the plague. Yes, that is what he used to do when he was bored.
Today, we have been able to calculate the value of 𝞹 to more than 2 trillion digits.
But why do we continue to do so if 𝞹 never ends?
The maximum value of 𝞹 needed for practical calculations is 3.141592653589793. This is the value engineers at NASA use for calculations in space.
Today, calculating 𝞹 to more and more digits has become a way to test the processing power of computers and set records.
Even, memorizing the maximum digits of 𝞹 has become a competition.
Rajveer Mina holds the world record for memorizing 70,000 digits of 𝞹 (it took him 10 hours just to recite them).